Weighting Factors for Games Played

Beginning with basketball results reported February 2, 2009, team strength ratings are calculated using weighting factors applied to games played during the season. Two weighting factors are applied, one based on the score difference in each game, and one based on how recently the game was played.

The score-based weighting factor is intended to obtain results where the program has worked harder to model score differences for games that are close than it does for games that are blowouts. In NM basketball, most of the games played have winning margin of 15 points or larger. A quarter of the games have winning margins of 25 points or more. The larger the score difference, the more likely it is that the coach of one or both teams adjusts the team's playing strategy to allow players with less experience to participate. As a result, the final score margin is likely to be larger or smaller than it would have been if the playing strategy was constant throughout the game.

The time-based weighting factor is intended to obtain results where the program has worked harder to model score differences for recently played games than it did for games played early in the season. Much about a team's playing composition can change during a season. Key players can become sick or injured or ineligible or otherwise unavailable to play for several games. Key players can return to play after an absence. A team can become more effective playing together as the season progresses, as players learn each other's strengths and how to use them effectively.

The combined weighting factor for any game is then the product of these two factors, leading to results that count recently played close games considerably more than it does early season blowouts.

Downside of Weighting Games. The downside of weighting games is that it requires some intuition to devise an appropriate form for the weighting function. The form chosen make elements of the algorithm heuristic. So, how do we invent weighting functions?

For both the score-based and time-based factors, we assume a normal probability distribution for both games scores and time-relevance of games. The normal probability distribution function is assumed for both factors.

Finding parameters to construct the score-based weighting function is easiest -- we look at all the (BV or GV) games played, and construct a normal probability distribution to fit the observed score distribution. The figure below shows a histogram plot of BV and GV game score differences in NM.

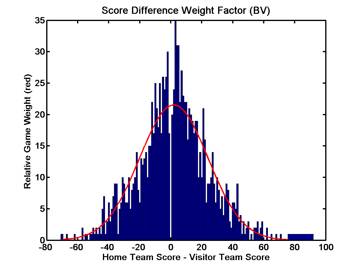
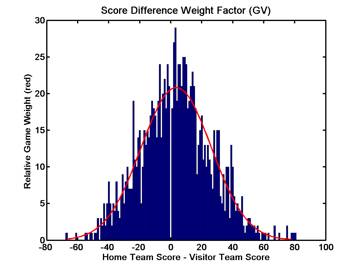
In each plot, you can see the distribution of game score differences, along with a plot of the bell-shaped gaussian curve that best fits this distribution. In each case, the mean of the distribution is about 2 points, which is what we use as a reasonable initial guess for home court advantage. The standard deviation of each distribution is about 22 points, which means about two-thirds of all games are closer than that, and one-third are won by margins in excess of 22 points.

We use the red curve shown in these plots as the relative weighting factor for games, based on score. Games won by 22 points (after removing the home court advantage) are weighted by 37% of those that would be ties (if ties were allowed -- note that both plots show no games that were tied).

Finding parameters for the time-based weighting factor is less satisfactory. We simply decide to say that games played on the first day of the season will count only half as much as games played on the last day of play (so far). The next two plots show the distribution of games played during the season, with this emprical weighting function superimposed in red.

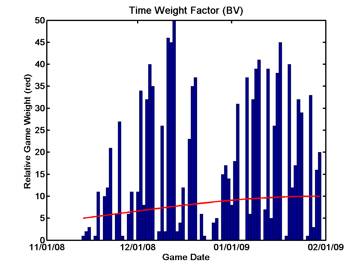
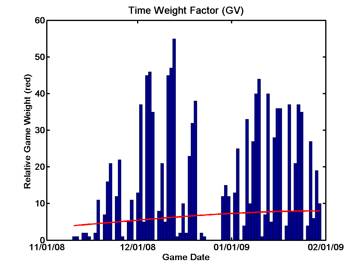
On the team schedule pages, the actual weighting factor associated with each game is now shown in its own table column.